bionpromo.blogg.se

Beyond the proof provided by the towering pyramids which still stand today, we also know that the ancient egyptians also knew how to: The Egyptians were also skilled geometricians. And for that their system made perfect sense. They were dealing with the trade and distribution of goods in a non-monetary economy. I wouldn’t want to do calculus using only the tools that the Egyptians had, but then again, they weren’t doing calculus.

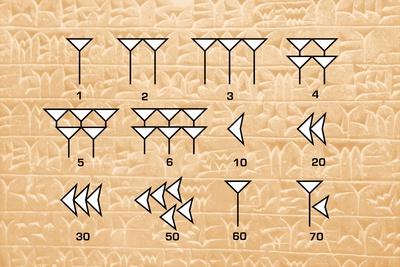
This brings up an important point: the number systems and mathematical procedures of a culture are a reflection of the practices of that culture. I’m not sure what I’d do with 1/30 of a loaf, but you can see that this would likely appear to be a fairer result in the end, if only because each person’s share would look similar. The other three workers would receive four pieces, two 1/3 pieces, a single 1/5 piece, and a single 1/30 of a loaf. The Egyptian form of division, strange as may seem to us today, would’ve resulted in the following result: seven workers would receive three pieces, 2/3, 1/5, and 1/30 of a loaf. Needless to say, this last worker may not think this was a fair deal (who likes the heal?). One way to do this equally would be to cut a tenth of each loaf, distribute the nine-tenth shares to nine workers, and then the nine one-tenth shares to the remaining worker. Each worker would receive nine-tenths of a loaf of bread. In a particularly interesting example from the text, imagine you’re an employer and you need to distribute nine loaves of bread among ten workers. As such, one might be paid for labor in the two most common goods of transaction: bread and beer. The unit fractions part is interesting because the ancient Egyptians did not use printed currency. This entailed a sequence of steps to solve a problem, but no operators such as +, -, etc. Practiced rhetorical (rather than symbolic) algebra.Made extensive use of unit fractions like ½, though avoided non-unit fractions like ¾ (though ⅔ apparently saw wide use).Were aware of the concept of zero but did not use it as a place value.Used a ciphered, non-place value, decimal numbering system.Much can be gleaned from the Ahmes and Moscow papyri.

The Moscow Papyrus, so-called because it is currently housed there, dates to around 1850 B.C.E. It measures 13 inches tall and nearly 16 feet long. It has been dated to approximately 1550 B.C.E.Ī portion of the Ahmes Papyrus. The Ahmes Papyrus, also known as the Rhind Papyrus (because it was owned at one time by a man named Alexander Rhind) may have been used as a teacher’s manual. Unfortunately, papyrus degrades over time and so much of what likely existed at the time of the ancient Egyptians has been lost. Now to the math, in which we’ll be compressing several thousand years of human development and many kingdoms into “Ancient Egypt” and “Mesopotamia.” Math of Ancient EgyptĪncient Egyptians wrote on papyrus, a thick, plant-based paper. If I were teaching a class on these subjects, this would be one of the first points I’d bring up. But the implications on our general understanding of the world are huge. The third chapter of The Crest of the Peacock by George Gheverghese Joseph, which focuses on the mathematical developments of the Egyptian empires, starts with that important, and often-ignored point.ĭoes it matter from a mathematical perspective that much of our mathematical tradition originated in Africa? I don’t know. From Egyptian Frustums to Babylonian Sexagesimal Jan 23, 2019īefore diving into the mathematics of the ancient Egyptians, here’s an important question: Were they African? Let’s check a map: